Combinatoric Holonomy
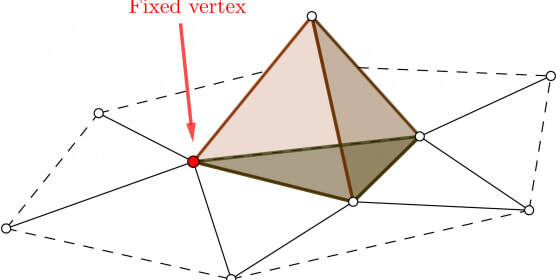
The concept of holonomy explores how smooth surfaces interact against each other by “rolling” one surface over another through arbitrarily closed loops around a base point. In our project, we focused on the discrete setup of this problem, in particular, we referred to triangular surfaces where we put an interaction between two surfaces by choosing two different faces of each one and matching vertices between them. This choice of two touching faces and the matching between their vertices define a position between the two surfaces. So our general goal of understanding the interaction between two surfaces is to figure out how the position changes after rolling the surfaces over each other, what are all possible positions we can get after rolling in arbitrary loops.
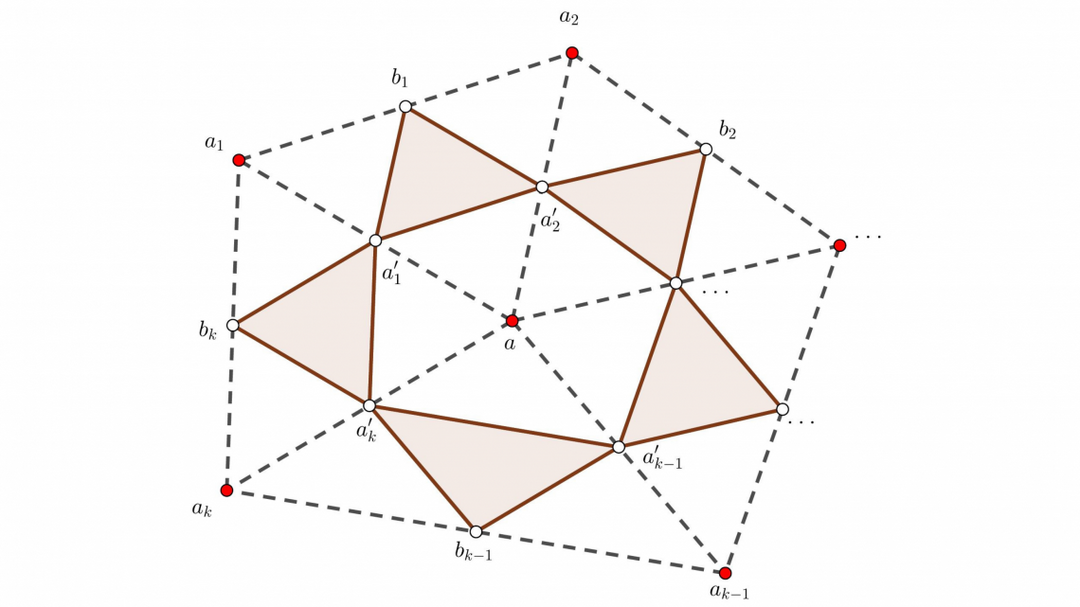
To understand the big picture, we started by making observations for a simple, highly symmetric structure - the tetrahedron - and examining what possible holonomy groups we can get from rolling it over different surfaces. Along with that, we built up our understanding of loop structure on a given surface, conjecturing about what features that loops may have and how those features give us computational tools to break down the holonomy group. Then, we introduced the concepts of contractibility and combinatorial fundamental group, brought from a perspective of algebraic topology. It helped us slightly reduce the complexity of calculating the holonomy groups. We then managed to develop mathematical tools using those ideas and apply them to compute the holonomy of triangular tori by looking at the generating elements induced by non-contractible loops. This gave us a classification of tori’s holonomies that vary from trivial, ℤ/2ℤZ/2Z, V4V4, to full tetrahedral groups. In the end, to identify surfaces that have the ℤ/3ℤZ/3Z holonomy, we introduced an entirely different method by dealing with the structure on the vertices of the surface. This method can identify exactly trivial or ℤ/3ℤZ/3Z holonomy for the orientable surface. Then, we used subdivided surfaces to apply this method and showed an example of a surface with ℤ/3ℤZ/3Z holonomy.
| Combinatorial Holonomy Final Presentation |
| Combinatorial Holonomy Write Up |
This video is my entry into the Khan Academy Breakthrough Challenge in 2018. I aimed to comically represent the history of Newton and Leibniz's unique derivation of Calculus.
International Mathematical Modeling Challenge 2019
In 2019, along with 3 other school colleagues we entered the IMMC 2019 and became National finalists.
We had to determine how many people Earth would hold. This involved us doing research and calculating the area necessary for crops, housing, animals and much more!
It was an intense and exciting experience and I would highly recommend it to anyone who wants to really push their mathematical ability.
We had to determine how many people Earth would hold. This involved us doing research and calculating the area necessary for crops, housing, animals and much more!
It was an intense and exciting experience and I would highly recommend it to anyone who wants to really push their mathematical ability.